4. 상관분석

상관분석은 두 연속형 변수 간의 선형적 관계의 방향과 강도를 수치로 나타내는 통계적 분석 방법입니다. 데이터과학과 통계학에서 두 변수 간의 관련성을 파악할 때 널리 사용되며, 변수 간에 상관관계가 존재한다고 해서 인과관계가 있는 것은 아닙니다. 인과관계를 분석하기 위해서는 회귀분석이 필요하며, 이는 다음절에서 다룹니다.

상관계수(Correlation Coefficient, Pearson’s r)

값의 범위: -1 ~ +1
+1: 완벽한 정(+)의 선형 관계
-1: 완벽한 부(-)의 선형 관계
0: 선형관계 없음

산점도 행렬(Scatter Plot Matrix)

산점도 행렬은 여러 변수 간의 쌍(pairwise) 관계를 시각적으로 확인할 수 있는 유용한 도구입니다. 각 셀에는 두 변수 간의 산점도가 나타나며, 경우에 따라 상관계수도 함께 표시됩니다.

예시: R의 mtcars 데이터셋 R의 기본 내장 데이터셋인 mtcars를 활용하면 다음과 같은 관계를 시각적으로 확인할 수 있습니다:

disp(배기량)와 cyl(실린더 수)간 강한 양의 상관관계
cyl은 이산형 변수이므로 산점도에서 점들이 일정한 위치에 정렬

# 데이터 불러오기
data(mtcars)

# 산점도 행렬 시각화
pairs(mtcars,
      main = "Scatter Plot Matrix of mtcars",
      pch = 21,
      bg = "lightblue",
      col = "black")

# GGally 패키지를 활용한 고급 시각화
install.packages("GGally") # 최초 1회만 실행
library(GGally)

# ggpairs 함수로 상관계수 및 산점도 함께 출력
ggpairs(mtcars,
        title = "GGally Scatter Plot Matrix with Correlations")

The downloaded binary packages are in
	/var/folders/7b/6s43j55556d1qtk2kmm3gdlw0000gn/T//RtmpF5yQOC/downloaded_packages

png

구조:

하단 삼각형: 산점도 (scatter plot)
상단 삼각형: 상관계수 (Pearson’s r) + 유의수준
대각선: 변수의 분포 (히스토그램 또는 밀도곡선)

표기 해석:

Corr: 0.868** -> 상관계수: 0.868, p-value < 0.01(통계적으로 유의미함)

변수1	변수2	상관계수	해석
mpg	wt	-0.868**	무게가 증가할수록 연비가 감소 (강한 음의 상관관계)
cyl	disp	0.902**	실린더 수가 많을수록 배기량이 큼 (매우 강한 양의 상관관계)
hp	carb	0.750***	마력과 카뷰레터 수 사이에 강한 양의 관계
wt	disp	0.888***	무게가 클수록 배기량도 큼 (자동차 크기 관련 변수)
mpg	cyl	-0.852**	실린더 수가 많을수록 연비는 낮아짐

피어슨 상관분석(Pearson Correlation Analysis)

피어슨 상관분석은 연속형 변수 두 개 간의 선형적 관계의 방향과 강도를 측정하는 모수적(parametric) 방법입니다. 가장 널리 사용되는 상관 측정 방식이며, 두 변수 모두 정규분포를 따른다는 가정이 필요합니다.

피어슨 상관계수:

$$ r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}} $$

$x_i$, $y_i$: 각 변수의 관측값
$\bar{x}$, $\bar{y}$: 각 변수의 평균
$r$: Pearson’s correlation coefficient

가정 조건(Assumptions)

피어슨 상관계수는 다음의 통계적 가정을 만족해야 신뢰할 수 있는 결과를 제공합니다.

선형성(Linearity): 두 변수 간 관계가 직선 형태여야 함
정규성(Normality): 각 변수는 정규분포를 따라야 함 (특히 작은 표본일 때)
등분산성(Homoscedasticity): 잔차의 분산이 일정해야 함
이상치 없음(No significant outliers): 이상치는 상관계수를 왜곡할 수 있음
연속형 변수(Interval/Ratio scale): 순서형/명목형 데이터에는 부적절

X <- c(1, 2, 3, 4, 5)
Y <- c(3, 6, 4, 9, 8)
cor(X, Y, method = 'pearson')

0.806225774829855

스피어만 상관분석(Spearman’s Rank Correlation)

스피어만 상관분석은 순서형 데이터 또는 비선형 관계를 갖는 연속형 변수 간의 단조(monotonic) 관계의 방향과 강도를 측정하는 비모수적(non-parametric) 방법입니다. 변수 간의 관계가 선형이 아니거나 정규성을 따르지 않을 경우 피어슨 상관분석보다 적합합니다.

주요 특징

데이터를 순위(rank)로 변환하여 계산
정규성, 등분산성, 선형성 가정 불필요
변수 간 단조 증가 또는 감소 관계만 있어도 사용 가능
이상치에 강건함(robust to outliers)

스피어만 상관계수:

$$ \rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} $$

$d_i$: 각 관측치의 순위 차이
$n$: 관측치의 개수
$\rho$: 스피어만 순위 상관계수 (Spearman’s ρ)

해석 기준

계수 범위	해석
0.90 ~ 1.00 또는 -0.90 ~ -1.00	매우 강한 단조 관계
0.70 ~ 0.89 또는 -0.70 ~ -0.89	강한 단조 관계
0.40 ~ 0.69 또는 -0.40 ~ -0.69	중간 정도의 단조 관계
0.10 ~ 0.39 또는 -0.10 ~ -0.39	약한 단조 관계
-0.09 ~ 0.09	거의 없음 또는 무관계

# 데이터 예시
x <- c(1, 2, 3, 4, 5)
y <- c(3, 6, 4, 9, 8)

# 스피어만 상관계수 계산
cor(x, y, method = "spearman")

# 유의성 검정 포함
cor.test(x, y, method = "spearman")

0.8

	Spearman's rank correlation rho

data:  x and y
S = 4, p-value = 0.1333
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho 
0.8 

해석

ρ = 0.8 → 변수 x와 y 간에 강한 양의 단조 상관관계가 있습니다.
→ 즉, x가 증가할수록 y도 증가하는 경향이 일관되게 존재합니다.
p-value = 0.1333 > 0.05
→ 그러나 이 상관관계는 통계적으로 유의하지 않음
→ 즉, 표본 수가 작거나, 우연일 가능성을 배제할 수 없음

상관분석 실습

10명의 학생을 대상으로 한 학습 시간(시간)과 시험 점수(점) 데이터가 아래와 같이 주어졌습니다. 이 두 변수 간에 상관관계(선형적 관계)가 존재하는지 확인하기 위해 피어슨 상관분석을 실시합니다.

	1	2	3	4	5	6	7	8	9	10
학습 시간(시간)	8	6	7	3	2	3	2	7	2	3
점수(점)	33	22	18	6	23	10	9	30	11	13

# 1. 패키지 불러오기
library(ggplot2)
library(showtext)

# 2. AppleGothic 폰트 등록 (Mac에 기본으로 있음)
font_add("apple", "/System/Library/Fonts/Supplemental/AppleGothic.ttf")
showtext_auto()

# 3. 데이터
time <- c(8, 6, 7, 3, 2, 3, 2, 7, 2, 3)
score <- c(33, 22, 18, 6, 23, 10, 9, 30, 11, 13)
df <- data.frame(time, score)

# 4. 산점도 시각화
ggplot(df, aes(x = time, y = score)) +
  geom_point(size = 3, color = "blue") +
  labs(title = "학습 시간과 시험 점수의 관계",
       x = "학습 시간 (시간)",
       y = "점수 (점)") +
  theme_minimal(base_family = "apple")

# 피어슨 상관계수 계산
cor(time, score, method = "pearson")

# 상관 유의성 검정
cor.test(time, score, method = "pearson")

0.7611402008388

	Pearson's product-moment correlation

data:  time and score
t = 3.3193, df = 8, p-value = 0.01055
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.2525393 0.9401938
sample estimates:
      cor 
0.7611402 

png

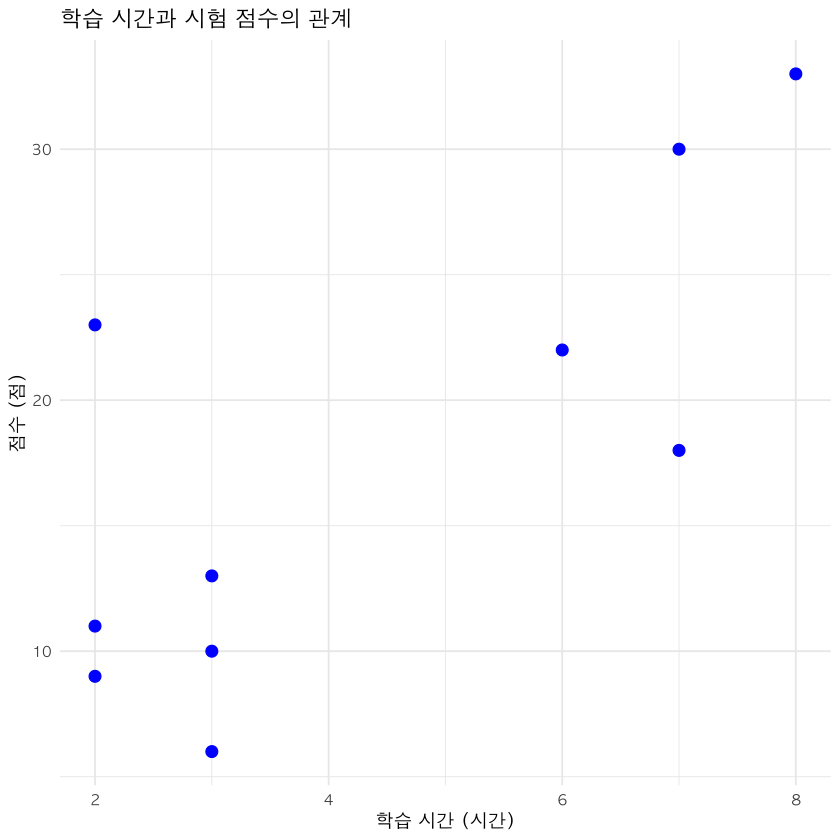
해석

상관계수 r = 0.761
→ 강한 양의 상관관계 존재(학습 시간이 늘어날수록 점수가 증가하는 경향)
p-value = 0.01055 < 0.05
→ 이 관계는 통계적으로 유의함
→ 귀무가설(H₀: 상관관계 없음)을 기각할 수 있음
신뢰구간 [0.253, 0.940]
→ 모상관계수가 이 구간 안에 있을 가능성이 95% → 즉, 상관관계가 우연이 아닌 일관된 패턴일 수 있음

학습 시간과 시험 점수 사이에 강한 양의 상관관계가 있으며, 이관계는 통계적으로 유의하므로, 학습 시간이 증가할수록 점수가 높아지는 경향이 있다고 해석할 수 있습니다.

상관분석

제2장 통계분석

목차