통계학 개론

1. 통계 개요

2. 확률과 확률분포

확률(Probability)

어떤 실험의 모든 가능한 결과들의 집합(표본공간, $S$) 중에서, 특정 사건 ($A \subseteq S$)가 발생할 가능성의 정도를 나타내는 수치입니다. 확률은 항상 0과 1 사이의 실수 값이며, 표본공간에 속한 모든 가능한 사건의 확률의 합은 항상 1입니다.

$$ 0 \leq P(A) \leq 1, \quad \sum_{i=1}^{n} P(A_i) = 1 \quad \text{(모든 가능한 사건 } A_i \text{에 대하여)} $$

조건부 확률(Conditional Probability):
특정 사건 A가 발생했다는 것이 사실이라는 전제하에 또다른 사건 B가 발생할 확률을 나타낸 값으로, 0과 1 사이의 값을 갖습니다.

$$ P(B \mid A) = \frac{P(A \cap B)}{P(A)}, \quad \text{단 } P(A) > 0 $$

기호	의미
$P(B \mid A)$	“A가 발생한 후 B가 발생할 확률”
$P(A \cap B)$	“A와 B가 동시에 일어날 확률”
$P(A)$	조건이 되는 사건 A의 확률 (분모)

독립사건(Independent Events)

확률론에서 두 사건 A와 B는 서로 독립(independent)이라고 할 수 있는 조건은 다음과 같습니다. 한 사건의 발생 여부가 다른 사건의 확률에 아무런 영향을 미치지 않아야 합니다. 즉, A가 일어났다는 사실을 알아도 B가 일어날 확률이 변하지 않아야 독립입니다.

정의 (Definition):
두 사건 A와 B가 독립일 필요충분조건은 다음과 같습니다:

$$ P(A \cap B) = P(A) \cdot P(B) $$

이는 “A와 B가 동시에 일어날 확률”이, “A가 일어날 확률과 B가 일어날 확률”의 곱과 같을 때 두 사건이 독립이라는 것을 의미합니다.

또는 조건부 확률을 사용한 표현으로 다음과 같습니다:

$$ P(B \mid A) = P(B) \quad \text{및} \quad P(A \mid B) = P(A) $$

배반사건 (Metually Exclusive Events)

확률론에서 두 사건 A와 B가 배반(mutually exclusive)이라고 할 때는, 둘 중 하나라도 발생하면 나머지는 절대 발생하지 않음을 의미합니다. 즉, 두 사건은 동시에 일어날 수 없습니다.

정의 (Definition):

두 사건 A와 B는 배반 사건일 때 다음 조건을 만족합니다.

$$ P(A \cap B) = 0 $$

이는 “A와 B가 동시에 발생할 확률”이 0이라는 뜻이며, 서로 겹치는 경우가 없음을 의미합니다.

또한, A와 B가 배반이라면, 둘 중 하나라도 발생할 확률은 다음과 같이 계산 됩니다:

$$ P(A \cup B) = P(A) + P(B) $$ 이는 두 사건이 겹치지 않기 때문에, 단순히 각 확률을 더하면 전체 확률이 된다는 뜻입니다.

확률변수(Random Variable)

확률변수는 확률 실험의 결과를 수치로 표현하는 함수입니다. 즉, 표본공간 $ \Omega $의 각 결과에 수치적인 값을 대응시키는 함수로서, 단순한 숫자가 아니라, 불확실한 실험 결과를 수학적으로 수치화한 함수입니다. 관측되는 데이터 값은 확률변수의 실현값(realisaition)입니다.

정의 (Definition):

A random variable is a function that assigns a real number to each outcome in a sample space:
-> 확률변수는 표본공간의 각 결과에 하나의 실수 값을 대응시키는 함수입니다.

$$ X : \Omega \rightarrow \mathbb{R} $$

$\Omega$: 표본공간 (Sample Space)
$X$: 확률변수
$\mathbb{R}$: 실수 집합

확률변수의 유형

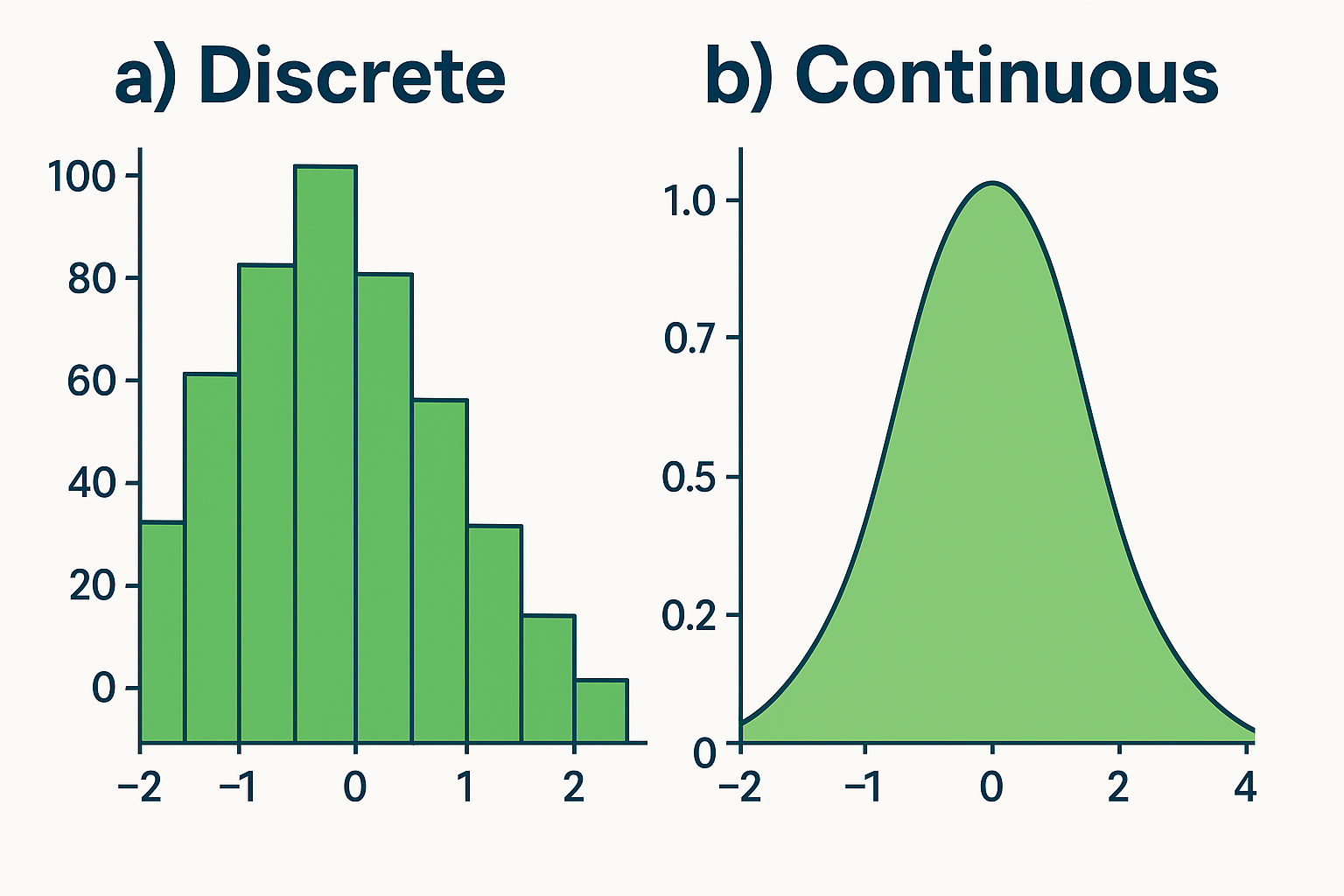
이산 확률변수 (Discrete Random Variable)
- 값이 셀 수 잇는 개수로 분리되어 있는 확률변수 입니다.
- 가능한 값들이 유한하거나 무한하지만 셀 수 있어야 합니다.
- 각 가능한 값에 확률을 직접 할당하며, 확률질량함수(PMF: Probability Mass Function)로 표현합니다. $$ P(X = x_i), \quad \sum_i P(X = x_i) = 1 $$
연속 확률변수 (Continuous Random Variable)
- 값이 연속적인 구간 내 모든 실수값을 취하는 확률변수 입니다.
- 특정(개별 실수) 값이 나올 확률은 항상 0이며($P(X = x) = 0$), 구간에 대한 확률만 정의됩니다.
- 확률은 확률밀도함수(PDF: Probability Density Function)로 표현합니다. $$ P(a \leq X \leq b) = \int_a^b f_X(x)\, dx, \quad \int_{-\infty}^{\infty} f_X(x)\, dx = 1 $$

확률분포 (Probability Distribution)

확률분포는 확률변수가 어떤 값을 가질 수 있으며, 그 각각의 값 혹은 구간에 어떤 확률이 할당되는지를 설명하는 수학적 규칙입니다. 확률변수가 이산형 혹은 연속형이냐에 따라 정의 방식이 달라집니다. 확률분포는 확률변수의 전체 행동을 설명하는 구조이며, 값의 분포 특성, 경향성, 불확실성의 형태를 모두 포함합니다.

표현식:

이산형: $$ \sum_i P(X = x_i) = 1 $$
연속형: $$ \int_{-\infty}^{\infty} f_X(x)\, dx = 1 $$

Probability Distribution

확률함수 (Probability Distribution)

확률함수는 확률변수의 값에 확률 또는 확률밀도를 할당하는 함수로, 이는 확률분포를 수학적으로 표한하는 도구 입니다. 확률변수의 유형에 따라 함수의 성격이 달라집니다.

정의 (Definition):

A probability function defines the likelihood that a random variable takes on specific values or falls within a giveen range.

즉, 확률함수는 확률변수의 값에 얼마만큼 확률이 할당되는지를 수치적으로 기술하는 함수입니다.

분류 (Types of Random Variables):

확률질량함수(Probability Mass Functionm, PMF)
- 이산 확률변수에 사용
- 각 가능한 값 $x$에 대해 확률 $P(X = x)$를 반환

$$ P(X = x), \quad \sum_x P(X = x) = 1 $$

확률밀도함수(Probability Density Function, PDF)
- 연속 확률변수에 사용
- 특정 값의 확률은 0이며, 구간에 대한 확률로 표현

$$ P(a \leq X \leq b) = \int_a^b f_X(x)\, dx, \quad \int_{-\infty}^{\infty} f_X(x)\, dx = 1 $$

기대값 (Expected Value)

이산형:
$\mathbb{E}[X] = \sum_x x \cdot P(X = x)$
연속형:
$\mathbb{E}[X] = \int_{-\infty}^{\infty} x \cdot f_X(x)\, dx$

분산 (Variance)

$\operatorname{Var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2]$

이상확률분포 (Discrete probability distributions)

베르누이 분포(Bernoulli Distribution)

정의(Definition):
하나의 시도(trial)에서 결과가 성공(1) 또는 실패(0) 두 가지 중 하나로만 나오는 상황을 수학적으로 모델링한 확률분포입니다.

확률변수: $X \sim \text{Bernoulli}(p)$
$p$: 성공 확률, $0 \leq p \leq 1$

확률질량함수 (PMF): $$ P(X = x) = p^x (1 - p)^{1 - x}, \quad \text{where } x \in {0, 1} $$ 기대값과 분산: $$ \mathbb{E}[X] = p, \quad \operatorname{Var}(X) = p(1 - p) $$

이항 분포(Binomial Distribution)

정의(Definition):
독립적인 베르누이 시행을 $n$번 반복하여 성공 횟수를 확률변수로 모델링한 분포입니다.

확률변수: $X \sim \text{Binomial}(n, p)$
$n$: 시행 횟수, $p$: 단일 시행의 성공 확률

확률질량함수 (PMF): $$ P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}, \quad k = 0,1,\dots,n $$ 기대값과 분산: $$ \mathbb{E}[X] = np, \quad \operatorname{Var}(X) = np(1 - p) $$

다항 분포(Multinomial Distribution)

정의(Definition):
다항 분포는 단일 시행에서 가능한 결과가 3개 이상인 사건을, $n$번 반복했을 때 각 결과가 나온 횟수의 분포를 모델링합니다. 이는 이항 분포의 일반화된 형태입니다.

확률변수:
$\mathbf{X} = (X_1, X_2, \dots, X_k) \sim \text{Multinomial}(n, p_1, p_2, \dots, p_k)$
조건:
$\sum_{i=1}^k X_i = n, \quad \sum_{i=1}^k p_i = 1$

확률질량함수 (PMF): $$ P(X_1 = x_1, \dots, X_k = x_k) = \frac{n!}{x_1! x_2! \dots x_k!} p_1^{x_1} p_2^{x_2} \dots p_k^{x_k} $$ 기대값과 분산: $$ \mathbb{E}[X_i] = n p_i, \quad \operatorname{Var}(X_i) = n p_i (1 - p_i) $$ 공분산 (i ≠ j): $$ \operatorname{Cov}(X_i, X_j) = -n p_i p_j $$

기하 분포(Geometric Distribution)

정의(Definition):
기하 분포는 독립적인 베르누이 실행을 성공할 때까지 계속 반복했을 때, 처음으로 성공이 나타나는 시행 번호를 확률변수로 표현한 분포입니다.

확률변수: $X \sim \text{Geometric}(p)$
$p$: 각 시행에서 성공할 확률

확률질량함수 (PMF): $$ P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}, \quad k = 0,1,\dots,n $$ 기대값과 분산: $$ \mathbb{E}[X] = np, \quad \operatorname{Var}(X) = np(1 - p) $$

포아송 분포(Poisson Distribution)

정의(Definition):
포아송 분포는 단위 시간 또는 단위 구간에서 발생하는 사건의 횟수를 모델링합니다. 주로 사건이 독립적으로 일정 비율로 발생하는 상황에서 사용됩니다.

확률변수: $X \sim \text{Poisson}(\lambda)$
$\lambda$: 단위 시간(또는 면적 등)당 평균 발생 횟수, $\lambda > 0$

확률질량함수 (PMF): $$ P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}, \quad k = 0, 1, 2, \dots $$ 기대값과 분산: $$ \mathbb{E}[X] = \lambda, \quad \operatorname{Var}(X) = \lambda $$

포아송 근사:

$n \to \infty, p \to 0, \lambda = np$ 고정일 때

$\text{Binomial}(n, p) \approx \text{Poisson}(\lambda)$

연속확률분포 (Continuous probability distributions)

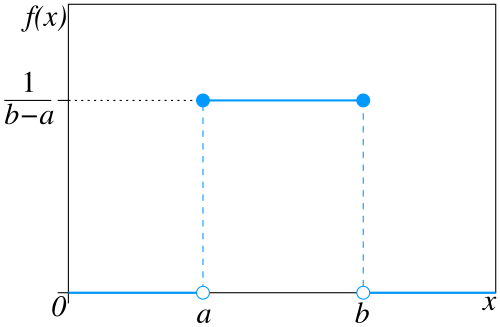
균등분포(Uniform Distribution)

정의(Definition):
균등분포는 모든 값이 동일한 확률로 발생하는 분포입니다. 연속 균등분포는 일정 구간 $[a, b]$ 내에서 값이 균등하게 분포한다고 가정합니다.

확률변수: $X \sim \mathcal{U}(a, b)$

확률밀도함수 (PDF):

Probability density function

기대값과 분산: $$ \mathbb{E}[X] = \frac{a + b}{2}, \quad \operatorname{Var}(X) = \frac{(b - a)^2}{12} $$

Uniform distribution

정규분포(Normal Distribution)

정의(Definition):
정규분포는 데이터가 평균을 중심으로 종형(bell-shaped) 곡선 및 대칭적으로 분포하는 분포입니다. 자연현상, 사회현상, 측정오차 등 다양한 데이터에서 중심극한정리에 의해 자연스럽게 나타납니다.

확률변수: $X \sim \mathcal{N}(\mu, \sigma^2)$
- $\mu$: 평균
- $\sigma^2$: 분산

확률밀도함수 (PDF): $$ f_X(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot e^{- \frac{(x - \mu)^2}{2\sigma^2} } $$

기대값과 분산: $$ \mathbb{E}[X] = \mu, \quad \operatorname{Var}(X) = \sigma^2 $$

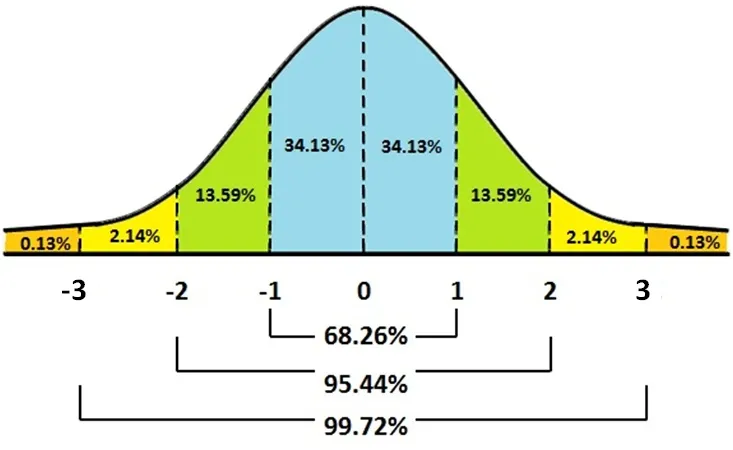
Normal distribution

표준정규분포:
정규분포는 평균 $\mu$, 표준편차 $\sigma$에 따라 곡선의 위치와 형태가 달라지므로, 확률변수 X가 특정 범위에 포함될 확률을 매번 직접 계산하는 것은 비효율적일 수 있습니다. 이러한 계산의 일관성과 편의를 위해 표준정규분포(Standard Normal Distribution)가 사용됩니다.

표준정규 분포는 평균이 0, 표준편차가 1인 정규분포를 의미하며, 다음과 같이 나타냅니다: $$ Z \sim \mathcal{N}(0, 1) $$

임의의 정규분포 $X \sim \mathcal{N}(\mu, \sigma^2)$를 다음과 같이 표준화(Standardisation)하면, 표준정규분포를 따르는 새로운 확률변수 $Z$로 변환할 수 있습니다. $$ Z = \frac{X - \mu}{\sigma} $$

표준화된 변수 $Z$에 대해선 표준정규분포(Z-table)를 이용해 누적 확률값을 손쉽게 계산할 수 있으며, 이는 통계적 추론과 가설검정의 기본 도구로 널리 사용됩니다.

t-분포(Student’s t-Distribution)

정의(Definition):
t-분포는 모평균(모수) 추정 시 모집단의 분산을 모를 경우 표본을 기반으로 추정할 때 사용되는 분포입니다. 표본의 크기가 작고, 분산이 알려지지 않은 상황에서 정규분포 대신 사용합니다.

특징: 중심은 0, 정규분포와 비슷하지만 꼬리가 두꺼우며, 자유도가 커질수록 정규 분포에 수렴합니다.

확률변수: $T \sim t_\nu, \quad \nu = \text{자유도 (degrees of freedom)}$

확률밀도함수 (PDF): $$ f_T(t) = \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi}\,\Gamma\left(\frac{\nu}{2}\right)} \left(1 + \frac{t^2}{\nu}\right)^{-\frac{\nu+1}{2}} $$

$\Gamma$: 감마 함수
$\nu$: 자유도 = n - 1

기대값과 분산: $$ \mathbb{E}[T] = 0, \quad \operatorname{Var}(T) = \frac{\nu}{\nu - 2}, \quad (\nu > 2) $$

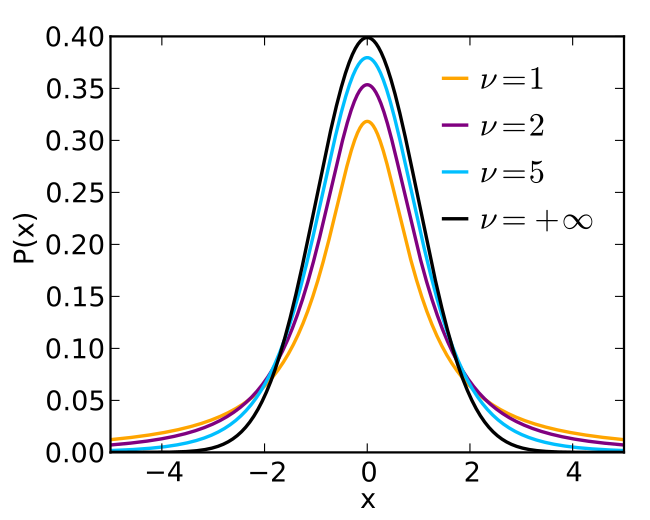
Student t-distribution

자유도(degrees of freedom, df)는 통계량을 계산하는 데 사용된 독립적인 정보의 개수를 의미합니다. 즉, 제약 없이 자유롭게 변할 수 있는 값의 수를 뜻합니다. 보통 “표본의 크기에서 제약 조건의 수를 뺀 값”으로 정의됩니다.

카이제곱 분포(Chi-squared Distribution)

정의(Definition):
카이제곱 분포는 표준정규분포를 따르는 독립 확률변수들의 제곱합으로 구성된 분포입니다. 주로 분산 추정, 적합도 검정($χ^2$ test), 독립성 검정, 동질성 검정 등에 사용됩니다.

동질성 검정(Test for Homogeneity)은 두 개 이상의 서로 다른 모집단이 같은 분포(또는 비율)를 가지는지 검정하는 방법입니다. 주로 범주형 데이터를 비교하며, 검정통계량은 카이제곱 분포를 따릅니다.

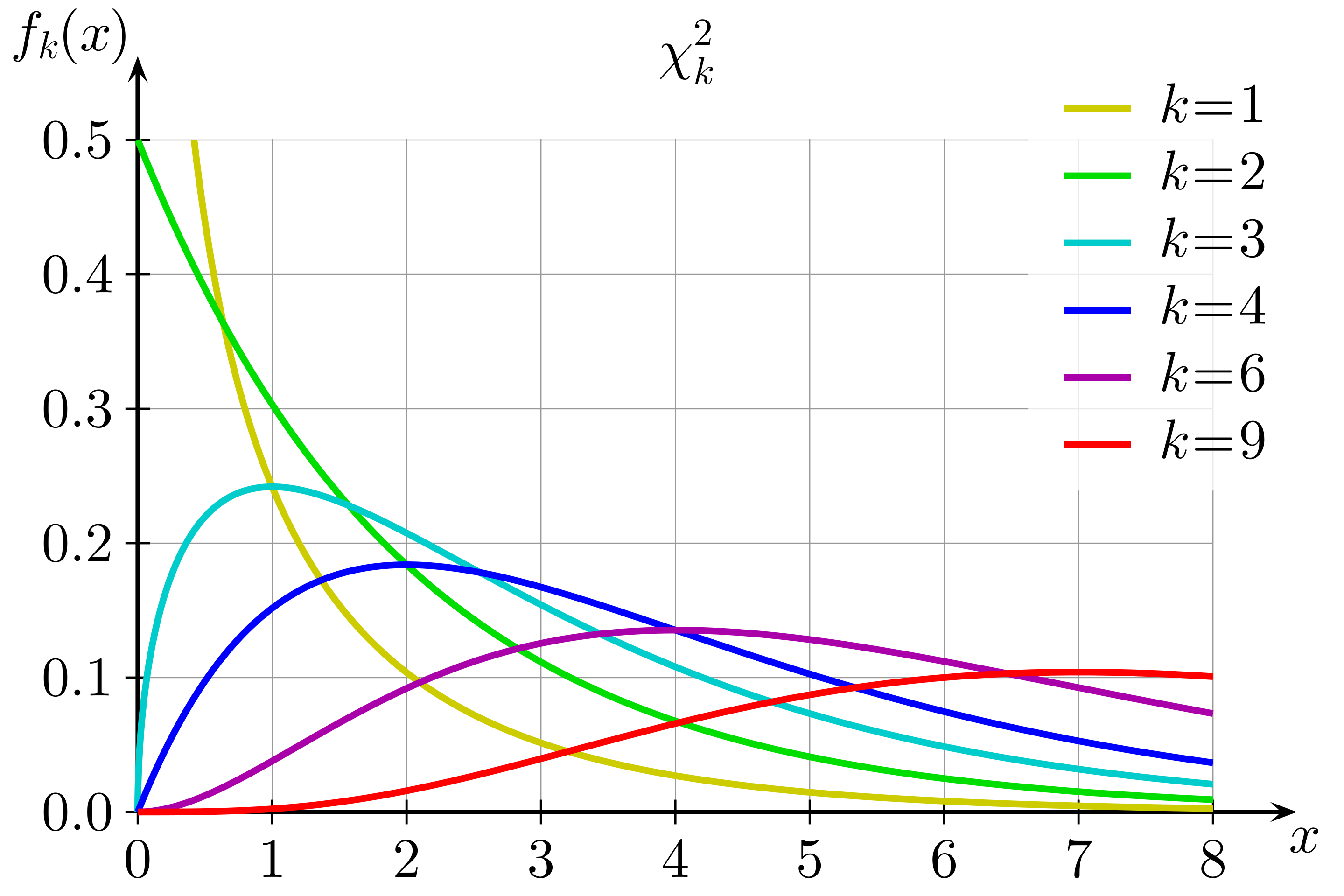
특징: 오른쪽으로 치우친 비대칭 분포(right-skewed)이며, 자유도가 커질수록 정규분포에 근사합니다.

확률변수: $X \sim \chi^2_k$
- $k$: 자유도 (degrees of freedom)
구성:
$X = \sum_{i=1}^{k} Z_i^2, \quad Z_i \sim \mathcal{N}(0, 1)$

확률밀도함수 (PDF): $$ f_X(x) = \frac{1}{2^{k/2} \Gamma(k/2)} x^{(k/2 - 1)} e^{-x/2}, \quad x > 0 $$

$\Gamma(\cdot)$: 감마 함수

기대값과 분산: $$ \mathbb{E}[X] = k, \quad \operatorname{Var}(X) = 2k $$

Chi-squared Distribution

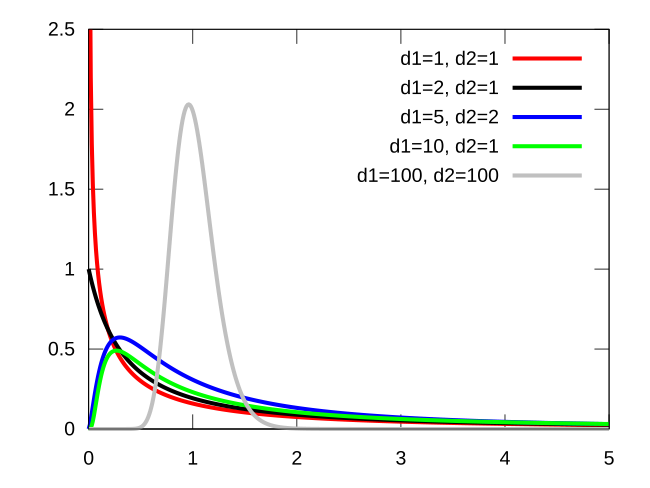
F-분포(F-Distribution)

정의(Definition):
F-분포는 두 카이제곱 분포를 각각 자유도로 나눈 값의 비율로 정의됩니다. 이는 주로 두 분산 간 비교(예: 등분산 검정), 분산분석(ANOVA)에서 사용됩니다.

등분산 검정(Homogeneity of Variance Test):
두 개 이상의 모집단이 동일한 분산을 가지는지를 검정하는 통계적 절차입니다. 이는 평균 비교를 위한 t-검정, ANOVA 등 가설검정 수행 전 필요한 사전 조건을 점검할 때 사용됩니다. 따라서, 두 모집단의 평균을 비교하는 경우, 예를 들어 t-검정, 회귀분석에서는 두 집단의 분산이 서로 동일하다는 가정이 필수적일 수 있어, 모평균 비교 전에 반드시 확인해야 할 전제 조건 입니다.

특징: 0보다 큰 값만 가지며, 오른쪽 꼬리가 긴 비대칭 분포입니다.$d_1, d_2$에 따라 형태가 달라집니다.

확률변수: $X \sim \chi^2_k$
- $k$: 자유도 (degrees of freedom)

확률밀도함수 (PDF): $$ f_F(x) = \frac{ \sqrt{ \frac{ (d_1 x)^{d_1} d_2^{d_2} }{ (d_1 x + d_2)^{d_1 + d_2} } } }{ x \cdot B(d_1/2, d_2/2) }, \quad x > 0 $$

$B(\cdot, \cdot)$: 베타 함수

기대값과 분산:

기대값 ($d_2 > 2$ 일 때): $$ \mathbb{E}[F] = \frac{d_2}{d_2 - 2} $$
분산 ($d_2 > 4$ 일 때): $$ \operatorname{Var}(F) = \frac{2 d_2^2 (d_1 + d_2 - 2)}{d_1 (d_2 - 2)^2 (d_2 - 4)} $$

F-Distribution

통계학 개론

제2장 통계분석

목차

1. 통계 개요

2. 확률과 확률분포

확률(Probability)

독립사건(Independent Events)

배반사건 (Metually Exclusive Events)

확률변수(Random Variable)

확률분포 (Probability Distribution)

확률함수 (Probability Distribution)

이상확률분포 (Discrete probability distributions)

베르누이 분포(Bernoulli Distribution)

이항 분포(Binomial Distribution)

다항 분포(Multinomial Distribution)

기하 분포(Geometric Distribution)

포아송 분포(Poisson Distribution)

연속확률분포 (Continuous probability distributions)

균등분포(Uniform Distribution)

정규분포(Normal Distribution)

t-분포(Student’s t-Distribution)

카이제곱 분포(Chi-squared Distribution)

F-분포(F-Distribution)