결측값 처리와 이상값 검색
제1장 R 기초와 데이터 마트
목차
1. 탐색적 데이터 분석(EDA)
탐색적 데이터 분석(EDA, Exploratory Data Analysis)이란 본격적인 분석이나 모델링에 앞서 데이터를 직관적으로 이해하고, 숨겨진 패턴이나 이상값(Outliers), 결측값(Missing values), 변수 간 관계(변수 간 상관성 등)를 시각적 및 통계적으로 탐색하는 과정입니다. 이 과정은 데이터의 분포, 범위, 중심 경향성(평균, 중앙값), 변동성(분산, 표준편차) 등의 통계적 요약 정보뿐 아니라, 변수 간의 관계나 그룹별 특성 차이 등을 시각화 도구를 활용해 파악하는 데 중점을 둡니다.
탐색적 데이터 분석은 모델링의 성능을 높이고, 데이터 정제(Cleaning)와 전처리(Preprocessing) 과정에서 올바른 의사결정을 내리는 데 핵심적인 역할을 하며, 분석 목적에 부합하는 데이터 기반 인사이트를 발견하는 데 중요한 출발점입니다.
붓꽃(Iris) 데이터를 이용한 탐색적 데이터 분석의 예
붓꽃(Iris) 데이터는 통계학자 피셔의 붓꽃 분류 연구에 기반한 데이터로 R 실습에 자주 활용됩니다. 세 가지 붓꽃 종(Species)에 따른 꽃받침 길이(Sepal Length), 꽃받침 폭(Sepal Width), 꽃잎 길이(Petal Length), 꽃잎 폭(Petal Width)을 기록한 데이터입니다. 붓꽃 데이터는 R에 기본 데이터로 내장되어 있으며, iris라는 데이터프레임을 불러올 수 있습니다.
head(iris, 3)
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species | |
|---|---|---|---|---|---|
|
|
|
|
|
|
|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
# 기초 통계량
summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
Median :5.800 Median :3.000 Median :4.350 Median :1.300
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Species
setosa :50
versicolor:50
virginica :50
# 데이터 구조 파악
str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
2. 결측값
결측값(Missing Values)은 데이터셋 내에 값이 존재하지 않는 상태를 의미하며, 일반적으로 NA(Not Available)로 표시되지만 데이터 수집 방식에 따라 null, 빈 문자열(“”), 특정 숫자(-1, 9999 등) 등으로 표현되기도 합니다. 데이터 분석에서 결측값은 분석 결과의 왜곡을 초래할 수 있기 때문에, 사전에 이를 정확히 식별하고 적절히 처리하는 것이 매우 중요합니다.
일반적인 결측값 처리 방법은 다음과 같습니다:
- 삭제(Removal): 결측값이 적고 무작위(MCAR)일 경우 해당 행 또는 열을 삭제.
- 대체(Imputation): 평균, 중앙값, 최빈값, 그룹별 평균 등으로 결측값을 채움.
- 모델 기반 대체: 회귀, KNN, 다중 대체법(MICE) 등 통계 모델이나 머신러닝 기법을 활용한 대체.
또한, 결측 자체가 의미를 가질 수 있는 경우도 있습니다. 예를 들어 특정 민감한 설문 문항에서 결측값이 집중되었다면, 이는 해당 문항의 민감성 지표로 활용될 수 있습니다.
결측값 처리를 도와주는 대표적인 패키지로 다음이 있습니다:
-
Amelia: 다중 대체법(Multiple Imputation) 기반의 결측값 처리 패키지. -
DMwR2: KNN 기반 결측 대체, 이상치 탐지 등 데이터 마이닝 중심 기능 제공.
따라서, 결측값은 단순히 제거하거나 채우는 대상이 아니라, 데이터의 구조적 특성을 반영할 수 있는 중요한 신호로 인식되어야 합니다.
install.packages("Amelia")
also installing the dependency ‘RcppArmadillo’
# Amelia 패키지에 내장되어 있는 missmap은 데이터프레임에서 결측값이 어디에 존재하고 어떻게 분포되어 있는지 한눈에 시각화하여 사용자에게 보여준다.
copy_iris <- iris # 원본 데이터 유지
copy_iris[sample(1 : 150, 30), 1] <- NA # Sepal.Length에 30개의 결측값 생성
library(Amelia)
missmap(copy_iris)

결측값 대치 방법
단순 대치법(Listwise Deletion)
결측값이 존재하는 행(row) 또는 열(column)을 삭제하는 가장 기본적인 결측값 처리 방법입니다. 가장 손쉬운 처리 방법이지만, 결측값이 많은 경우 대량의 데이터 손실이 발생할 수 있으며, 분석의 통계적 대표성을 약화시킬 위험이 있습니다. 특히 데이터가 MCAR(Missing Completely At Random) 조건을 만족하지 않으면 편향(Bias)이 발생할 수 잇습니다. R에서는 complete.cases() 함수를 사용하여 결측값이 없는 행만 필터링 할 수 있습니다. 이 함수는 각 행을 검사하여 하나라도 NA가 존재하면 FALSE, 모든 열이 값이 있으면 TRUE를 반환합니다.
# 테스트를 위한 결측값을 가진 iris 데이터 생성
dim(copy_iris) # 기존 데이터 수
[1] 150 5
# Before deletion: check dimensions and number of complete cases
dim(copy_iris) # original dimensions
sum(!complete.cases(copy_iris)) # number of incomplete rows
# Apply listwise deletion (complete case analysis)
copy_iris_clean <- copy_iris[complete.cases(copy_iris), ]
# After deletion: check new dimensions
dim(copy_iris_clean) # dimensions after removing rows with NA
sum(!complete.cases(copy_iris_clean)) # return 0 (no missing values)
[1] 150 5
[1] 30
[1] 120 5
[1] 0
평균 대치법(Mean Imputation)
관측 또는 실험으로 얻은 데이터를 대표할 수 있는 평균(mean) 혹은 중앙값(median)으로 결측값을 대치하여 불완전한 자료를 완전한 자료로 만드는 방법입니다. 크게 비조건부 평균 대치법과 조건부 평균 대치법으로 구분 됩니다.
-
비조건부 평균 대치법(Unconditional Mean Imputation): 전체 데이터를 기준으로 계산한 평균 또는 중앙값을 결측값에 일괄적으로 대치합니다. 단순하지만 데이터의 분산을 과소추정할 수 있고, 예측 정확도에는 한계가 있습니다.
-
조건부 평균 대치법(Conditional Mean Inputation): 결측값이 포함된 변수와 다른 관련 변수 간의 관계(상관관계)를 이용하여 평균값을 예측한 뒤 대치합니다. 일반적으로 회귀분석(regression)을 통해 예측값을 산출합니다.
결측값을 수동으로 평균이나 중앙값으로 대치할 수도 있지만, 보다 간편하게는 DMwR2 패키지의 centralImputation() 함수를 활용할 수 있습니다. 이 함수는 수치형 변수에는 평균을, 범주형 변수에는 최빈값을 자동으로 결측값을 처리합니다.
최빈값(mode): 데이터에서 가장 자주 나타나는 값
참고: 평균 대치법은 데이터의 분포를 왜곡할 가능성이 있어, 예측 모형 학습 전에 영향도 분석 또는 보완적 방법과 함께 사용하는 것이 바람직합니다.
# 테스트를 위한 결측값을 가진 iris 데이터 생성
copy_iris <- iris # 원본 데이터 유지
copy_iris[sample(1 : 150, 30), 1] <- NA # Sepal.Length에 30개의 결측값 생성
# 평균 대치법
meanValue <- mean(copy_iris$Sepal.Length, na.rm = T) # 결측값을 제외한 평균 계산
copy_iris$Sepal.Length[(copy_iris$Sepal.Length)] <- meanValue # 평균 대치
# central Imputation을 활용한 중앙값 대치
library(DMwR2)
copy_iris[sample(1 : 150, 30), 1] <- NA
copy_iris <- centralImputation(copy_iris)
dim(copy_iris)
sum(!complete.cases(copy_iris))
[1] 150 5
[1] 0
단순 확률 대치법(Stochastic Imputation)
단순 확률 대치법은 평균 대치법(Mean Imputation)에서 발생할 수 있는 추정량의 표준 오차(standard error) 과소 추정 문제를 보완하기 위해 고안된 방법입니다. 이 방식은 단일 고정값이 아닌, 확률적 요소를 고려하여 결측값을 대치함으로써 데이터의 변동성과 불확실성을 일정 부분 반영할 수 있도록 설계되었습니다.
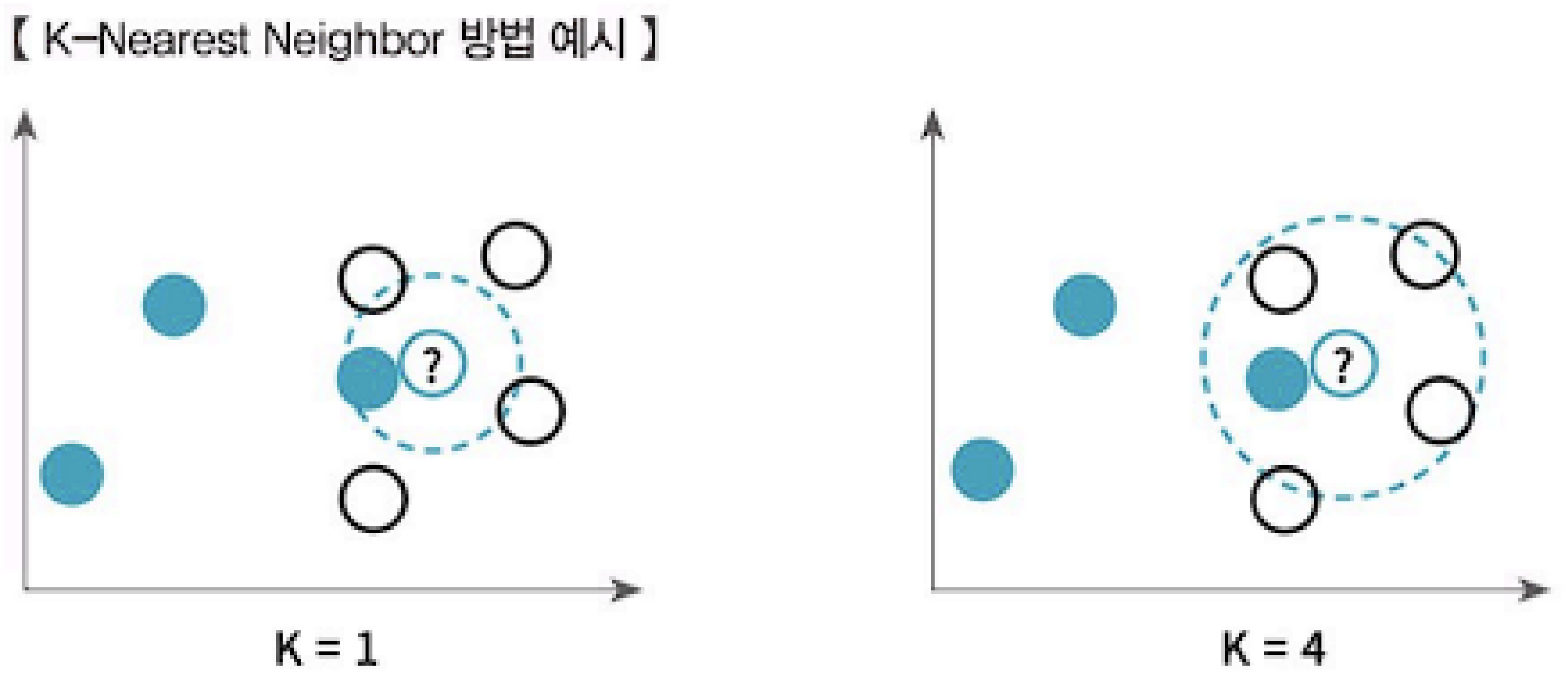
대표적인 방법으로는 K-최근접 이웃(K-Nearest Neighbors, KNN) 대치법이 있으며, 이는 관측된 데이터 중 결측값과 유사한 속성을 가진 K개의 이웃을 기준으로 값을 예측하여 결측치를 대치하는 방식입니다. 이와 같은 기법은 평균이나 중앙값 대치보다 더 유연하며, 다변량 관계를 어느 정도 보존할 수 있다는 장점이 있습니다.
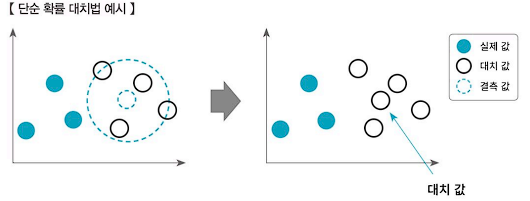
추정량의 표준 오차의 과소 추정 문제: 평균 대치법으로 결측값을 대치하면 n번을 수행하더라도 고정된 값을 갖습니다. 즉, 해당 결측값이 오차가 없다고 간주하게 됩니다. 이처럼 오차가 없다고 간주하는 것을 표준 오차의 과소 추정이라고 합니다. 따라서 확률분포를 기반으로 결측값을 대치하는 방법을 단순 확률 대치법이라 하며, K-NN은 K값에 따라 오차를 고려해 결측값을 대치할 수 있습니다.
KNN 대치법: K 최근접 이웃 알고리즘으로 주변 K개의 데이터 중 가장 많은 데이터로 대치하는 방법입니다. 아래 그림에서 K = 1인 경우 결측값으로 파란색이 유력해 보이지만 K = 4인 경우에는 결측값으로 검정색이 유력해 보입니다. 즉, K 값이 너무 작으면 이상치에 민감할 수 있으며, K 값이 너무 크면 근처 데이터들의 특성을 반영할 수 없기 때문에 적절한 K 값의 선정이 매우 어렵습니다.
# 테스트를 위한 결측값을 가진 iris 데이터 생성
copy_iris <- iris # 원본 데이터 유지
copy_iris[sample(1:150, 30), 1] <- NA
copy_iris <- knnImputation(copy_iris, k = 10)
다중 대치법(Multipe Imputation, MI)
다중 대치법은 결측값을 처리하는 통계적으로 강력한 방법으로, 하나의 결측값을 여러번 대치해 여러 개의 완전한 데이터셋을 생성한 뒤 이들을 분석하여 결과를 결합(combline)하는 방식 입니다. 이는 단순 대치법이 결측값의 불확실성을 반영하지 못하는 단점을 극복할 수 있습니다.
다중 대치법은 아래의 세 단계로 구성됩니다:
- 대치(Imputation): 결측값을 포함한 원본 데이터에서 M개의 서로 다른 대치 결과를 생성합ㄴ디ㅏ. 각 데이터는 결측값을 예측 모델(회귀, 로지스틱 회귀 등)을 기반으로 대치하여 완전한 형태로 만듭니다.
- 분석(Analysis): 생성된 M개의 완전 데이터셋 각각에 대해 동일한 분석 기법을 적용합니다.
- 결합(Pooling): M개의 분석 결과를 종합하여 최종 추론을 수행합니다. 평균, 분산 등을 종합할 때 Rubin’s Rule을 주로 사용합니다.
# 테스트를 위한 결측값을 가진 iris 데이터 생성
copy_iris <- iris # 원본 데이터를 유지
copy_iris[sample(1:150, 30), 1] <- NA
# Amelia 패키지 로드 및 다중 대치 수행
library(Amelia)
iris_imp <- amelia(copy_iris, m = 3, cs = "Species") # m: 대치 횟수, cs: 종단 단위 변수
# cs(cross-sectional identifier)은 동일 시점에 존재하는 서로 다른 개체들을 구분하기 위한 변수
# 위 amelia에서 m 값을 그대로 imputation의 데이터셋에 사용
copy_iris$Sepal.Length <- iris_imp$imputations[[3]]$Sepal.Length
-- Imputation 1 --
1 2 3
-- Imputation 2 --
1 2 3
-- Imputation 3 --
1 2 3
3. 이상값(Outlier)
이상값은 통계학 및 데이터 분석에서 다른 관측치와 비교하여 현저하게 크거나 작은 값을 의미합니다. 이러한 값은 측정 오류, 데이터 입력 오류, 자연스러운 변동성 등 다양한 원인에 의해 발생할 수 있으며, 데이터 분석 결과에 큰 영향을 미칠 수 있습니다. 따라서 이상값의 식별과 처리는 데이터 분석 과정에서 중요한 단계입니다.
이상값 판단
ESD(Extreme Studentised Deviation)
단일 변수 데이터셋에서 하나 이상의 이상값(Outlier)을 탐지하기 위한 통계적 방법입니다. 이 테스트는 정규 분포를 따른다는 가정 하에 수행되며, 특히 이상값의 개수를 미리 정확히 알기 어려운 경우에 유용합니다.
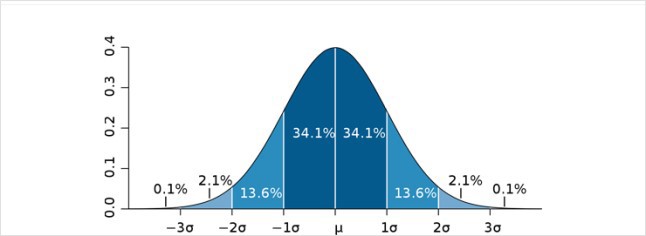
3-시그마(3-Sigma) 규칙과의 비교
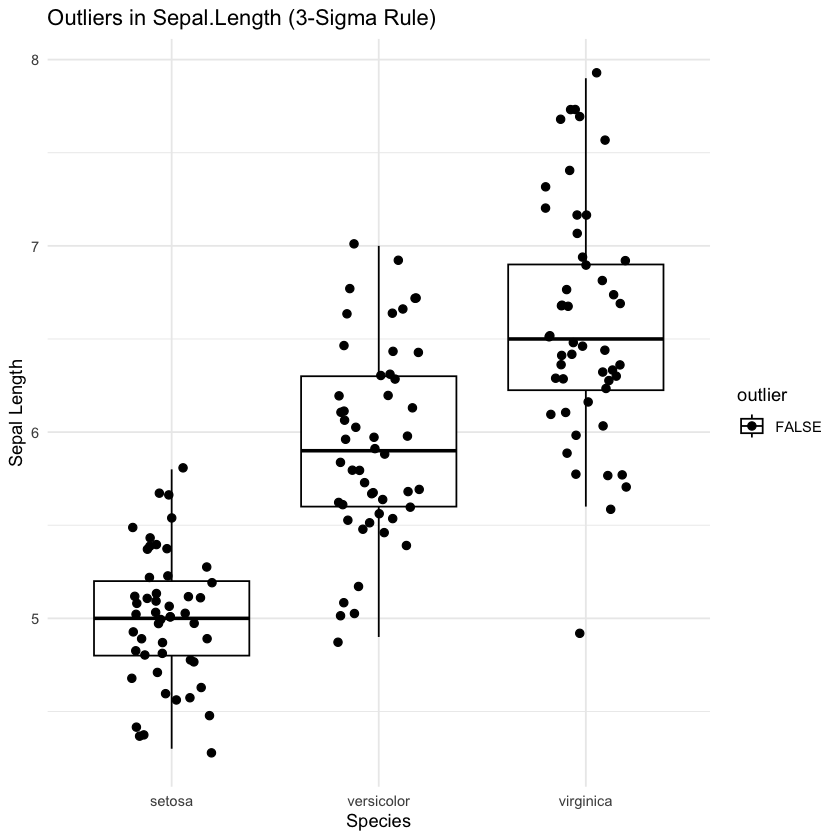
3-시그마 규칙은 데이터가 정규 분포를 따른다는 가정 하에, 평균으로부터 3배의 표준편차를 벗어나는 데이터를 이상값으로 간주하는 방법입니다. 이는 전체 데이터의 약 0.3%에 해당하며, 단순하고 직관적인 방법입니다. 그러나 이 방법은 이상값이 여러 개 존재하거나 데이터셋이 작은 경우에는 효과적이지 않을 수 있습니다.
# 데이터 로드
data(iris)
# ggplot2 설치 및 로드
if (!require("ggplot2")) install.packages("ggplot2")
library(ggplot2)
# 이상값 탐지 함수 (3-sigma 기준)
detect_outliers <- function(x) {
mu <- mean(x)
sigma <- sd(x)
lower <- mu - 3 * sigma
upper <- mu + 3 * sigma
return(x < lower | x > upper)
}
# Sepal.Length 기준으로 이상값 탐지
iris$outlier <- detect_outliers(iris$Sepal.Length)
# 시각화
ggplot(iris, aes(x = Species, y = Sepal.Length, colour = outlier)) +
geom_boxplot(outlier.shape = NA) +
geom_jitter(width = 0.2, size = 2) +
scale_colour_manual(values = c("black", "red")) +
labs(title = "Outliers in Sepal.Length (3-Sigma Rule)",
y = "Sepal Length") +
theme_minimal()
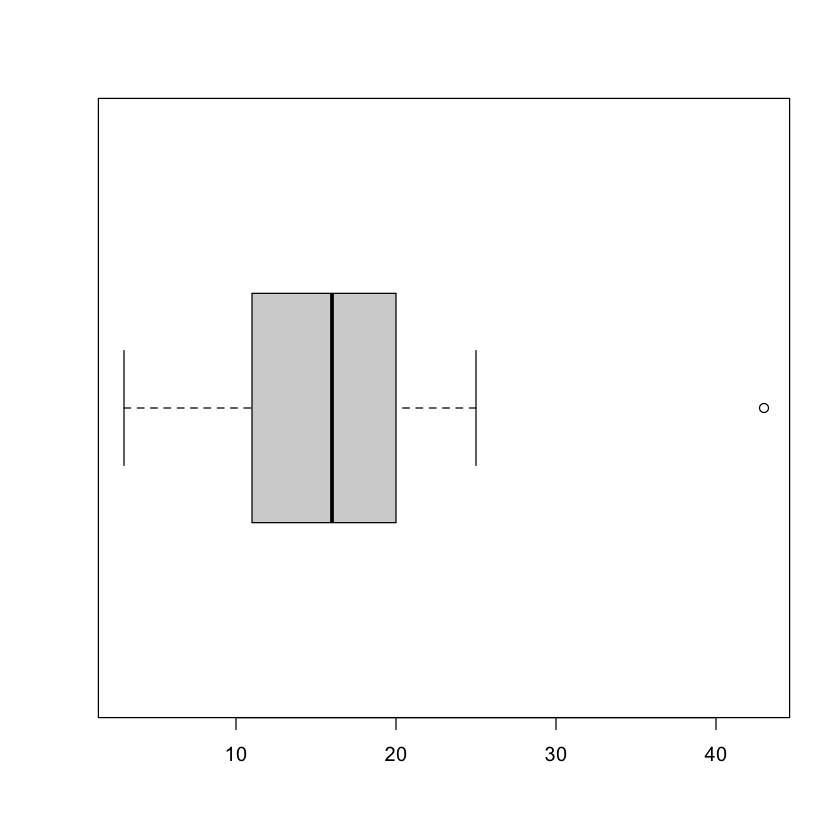
사분위수
사분위수를 이용하여 25%에 해당하는 값(Q1)과 75%에 해당하는 값(Q3)을 활용하여 이상치를 판단하는 방법입니다. 자료를 크기 순서대로 나열했을 때 다음 그림과 같이 사분위수로 나눌 수 있습니다. 가장 작은 하한 산분위수를 Q1이라고 하고, 가장 큰 사분위수인 상한 사분위수는 Q3라고 합니다. 여기서 IQR이란 사분위수의 정상 범위인 Q1과 Q3사이를 의미하며, 사분범위(Interquartile Range, IQR)라고 합니다. 이상치 판단 기준은 통계학자 John Tukey가 제안한 방식에 기반하여, 사분범위에서 1.5분위수를 벗어나느 경우 이상치로 판단합니다. 다시 말해 $Q1 - 1.5 \times IQR$(하한 최솟값)보다 작거나 $Q3 + 1.5 \times IQR$(상한 최댓값)보다 큰 값을 이상값으로 간주합니다. 시각적으로 상자 그림의 이상값(outliers)에 위치해 점으로 표현된 데이터를 이상값으로 판단됩니다.
사분위수: 측정값을 최솟값에서 최댓값까지 오름차순으로 정렬한 자료를 4등분했을 때 각 등분 위치에 해당하는 값을 의미합니다. IQR은 1분위 수(Q1)부터 3분위 수(Q3)까지의 범위를 의미하며, 2분위 수(Q2)는 중앙값(median)에 해당합니다.
# 테스트를 위한 임의 데이터 생성
data <- c(3, 10, 13, 16, 11, 20, 17, 25, 43)
boxplot(data, horizontal = T)